深度学习《自然语言处理理论与实战》pdf免费下载
计算：Ax-b
A: 2*2
x: 2*1
b: 2*1
so, Ax-b: 2*1
if __name__ == "__main__":
A = np.array([[4.0, 1.0],
[1.0, 3.0]])
b = np.array([[1.0], [2.0]])
x_0 = np.array([[2.0], [1.0]])
r_k = A * x_0 - b
print(r_k)
错误！！！
修改：
if __name__ == "__main__":
A= mat([[4.0, 1.0],
[1.0, 3.0]])
b = mat([[1.0], [2.0]])
x_0 = mat([[2.0], [1.0]])
r_k = A * x_0 - b
print(r_k)
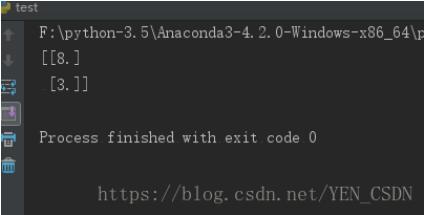
if __name__ == "__main__":
A= mat([[4.0, 1.0],
[1.0, 3.0]])
b = mat([[1.0], [2.0]])
x_k = mat([[2.0], [1.0]])
p_k = -x_k # 2行1列
r_k = A * x_k - b # 2行1列
alpha_k = (np.transpose(r_k) * r_k) / (np.transpose(p_k) * A * p_k) # 1行1列
-----------------------------------------------
x_k = x_k + alpha_k * p_k #2行1列 ！！！！这里报错
-----------------------------------------------
print(x_k)
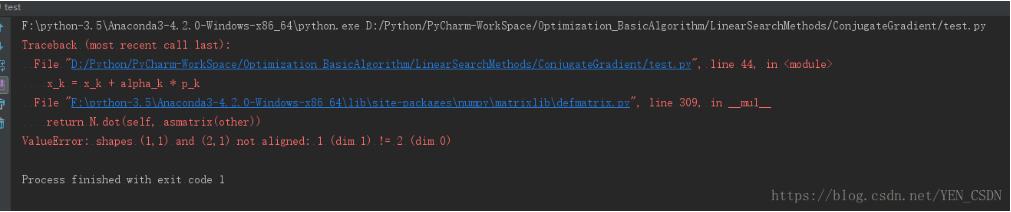
修改：
if __name__ == "__main__":
A= mat([[4.0, 1.0],
[1.0, 3.0]])
b = mat([[1.0], [2.0]])
x_k = mat([[2.0], [1.0]])
p_k = -x_k # 2*1
r_k = A * x_k - b # 2*1
alpha_k = (np.transpose(r_k) * r_k) / (np.transpose(p_k) * A * p_k) # 1*1
-----------------------------------------------
x_k = x_k + p_k *alpha_k
-----------------------------------------------
print(x_k)
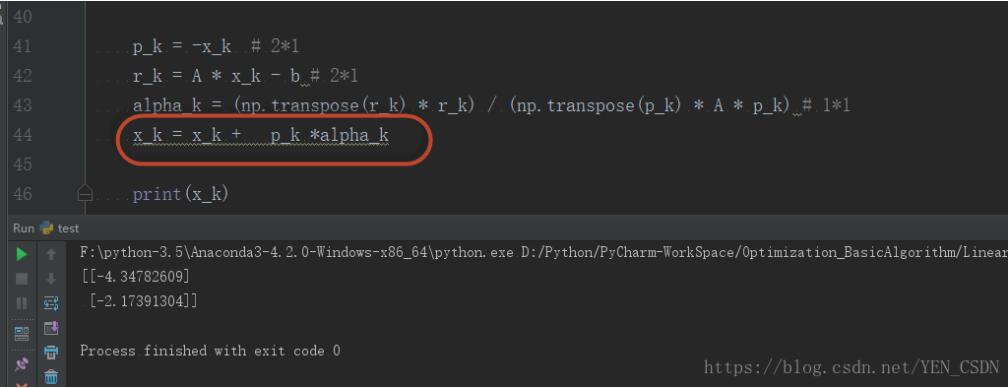
以上这篇解决Python计算矩阵乘向量,矩阵乘实数的一些小错误就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持谷谷点程序。
转载请注明：谷谷点程序 » 解决Python计算矩阵乘向量,矩阵乘实数的一些小错误